共通テスト　数学・記述式問題
大学入試改革　(3)

　緑地公園計画推進委員会が公表した、銅像の建立を含む整備計画の記事を読みながら、会話する花子さんと太郎さん。写真を撮るとき、「銅像」が最もよく見える位置はどこか―。文科省が公表した「高大接続改革の進捗状況について」（５月１６日）とともに、(独)大学入試センターが提供した記述式問題の「モデル問題例」の数学の問題。事象を数学化する力や問題解決までの構想力なども問われる。「大学入学共通テスト」（仮称）では、どんな能力を求められ、どういう点に配慮した指導が必要か。

マークシート式と混在
日常生活、社会事象も素材に
問題数３問程度、試験時間は７０分想定

　「大学入学共通テスト」（仮称）の目玉となる記述式問題。「数学」での出題科目は、「数学I」「数学I・数学Ａ」で、出題範囲は「『数学I』の内容」としている。共通必履修科目として設定し、記述式問題の意義が大きいと考えられている。
　過去の大学入試の問題を、

　(1)数学的に処理すること等によって、数値等の解答を得る
　(2)数学的な処理を行って解決して結果を得るために数式、図表、グラフなどで表現する
　(3)問題解決するに当たって把握すべき数学的な事柄・事実や、問題解決に向けた構想を立てることなどの問題解決の方略を表現する
　(4)いわゆる証明問題のように、問題解決のプロセス全体を表現する

　―に大別。
　作問検討チームは大規模共通試験の可能性なども加味して、(1)(2)に加え、(3)について条件付記述式として出題することとした。当面、(4)については「引き続き個別選抜で問うことが望ましい」としている。
　条件付記述式問題での素材選定の工夫例には「数学的な事象を扱ったもの」「日常生活、社会事象を扱ったもの」「図表やグラフなどを用いて考えたことが解答の前提となる問題」などを挙げた。
　「実施方針策定に当たっての考え方」（案）では、評価すべき能力などとして「図表やグラフ・文章などを用いて考えたことを数式などで表したり、問題解決の方略などを正しく書き表したりする力など」と明示し「特に、『数学を活用した問題解決に向けて構想・見通しを立てること』に関わる能力を重視する」とした。
　問題数は「３問程度」とし「大問の中にマークシート式問題と記述式問題を混在して出題」「試験時間はマークシート式と合わせて７０分程度とすることを想定している」。

指導のポイント

　「数学I」は数と式、図形と計量、二次関数、データの分析などを内容としている。
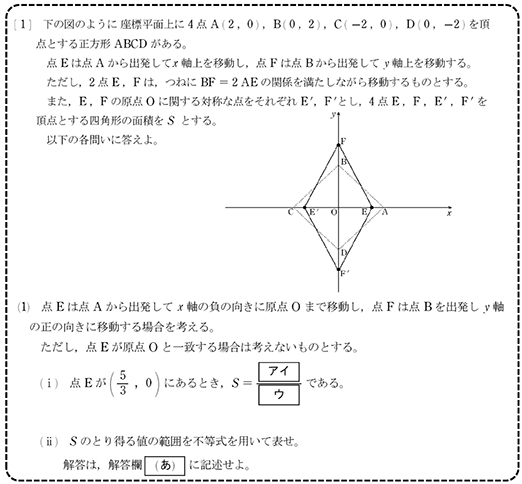
　「モデル問題例３」の〔１〕は「動点のつくる四角形の面積の変化を捉える場面」を素材に「自ら変数を設定し二次関数に対応づける構想力」「二次関数の式やグラフを活用して問題を処理する力」を問うとしている。
　センター試験との違いについては、センター試験が「問題解決の構想から結論に至るプロセスがすべて提示」されているのに対し、モデル問題例では「何を変数として設定するか、またそれを用いてどのように関数として表現・処理していくかなど、受験者の主体的な思考力を必要とする」と明示した。
　「記述せよ」と出題された〔１〕（１）（ii）での指導内容は学習指導要領「（３）二次関数　ア　二次関数とそのグラフ　事象から二次関数で表される関係を見いだすこと。また、二次関数のグラフの特徴について理解すること」と「（３）二次関数　イ　二次関数の値の変化　（ア）二次関数の最大・最小　二次関数の値の変化について、グラフを用いて考察したり最大値や最小値を求めたりすること」。
　「正答の要素」には「二次関数の式、グラフを活用して面積の変化を捉え、そのとり得る値の範囲を不等式で正しく記述することができる」を示す。
　同様に、〔２〕（４）は「（３）二次関数　イ　二次関数の値の変化　（イ）二次方程式・二次不等式　二次方程式の解と二次関数のグラフとの関係について理解するとともに、数量の関係を二次不等式で表し二次関数のグラフを利用してその解を求めること」が指導する内容。「三角比や正弦定理、余弦定理を用いて条件に適する図形やその特徴などを答える」ことが求められる。
　「モデル問題例４」の〔１〕（２）（i）は「三角形の一つの角が鋭角であることを確かめる方法として、余弦定理から得られる３辺の長さについての関係を用いて調べるという方略（構想）を見いだす力を問う」ことが狙い。
　同じく〔１〕（２）（ii）は「三角形において一辺の長さが固定されているとき、その対角が最大となる場合は外接円の半径が最小となること、正弦定理を根拠とすればよいことを見いだす力を問う」とした。
　指導内容は〔１〕（２）（i）、〔１〕（２）（ii）ともに「（２）図形と計量　イ　図形の計量　三角比を平面図形や空間図形の考察に活用すること」である。

　モデル問題例３

　モデル問題例４