数学I・数学A
須田　学　　筑波大学附属駒場中・高校教諭
判別式を多面的に捉える

　プレテスト第１問（必答問題）の［１］は、コンピュータのグラフ表示ソフトを利用する場面で、二次関数の係数の値の変化に伴ってグラフが移動する様子を考察する問題でした。正答率は（１）５０・９％、（２）７８・５％、（３）４４・８％、３４・９％、（４）２・０％（記述式）という結果で、他の問題と比べると高い数値となりました。
　公表された問題のねらいには「単に計算によって式や数値を求める問題とならないように工夫」「論理的に推論したり解決過程を振り返ったりしながら、見いだした事柄の根拠を数学的な表現を用いて説明する力を問う」という記述があります。現行の大学入試センター試験のように定型的に「平方完成して頂点を求めて…」というような流れを見せない形式になっているので、標準的な解き方だけを学習している生徒には、特に（３）（４）は難しかったと思われます。
　一方で、b〔2〕―4acの意味を単に判別式としてだけでなく、「頂点のｙ座標に含まれる式」「ｘ軸との交点のｘ座標に含まれる式」のように多面的に理解していた生徒にとっては、計算量も少なく、解きやすい出題だったはずです。
　特に、「GeoGebra」や「GRAPES」などのグラフ表示ソフトを操作する様子を見たり、実際に操作したりした経験があれば、問題の設定は容易に把握できました。

確認→標準的な証明→他の考え方の手順

　ここでは、生徒１人で１台のコンピュータ（パソコン、タブレットなど）を利用する環境を想定して授業を計画しました。
　グラフ表示ソフトは、さまざまなOSでインストール可能なフリーソフト「GeoGebra」を想定しています。インストールが難しい環境であれば、インターネットに接続して、ブラウザで「https://www.geogebra.org/graphing」にアクセスして利用することもできます。コンピュータの台数に制限があるのであれば、グループワーク形式にしてもよいでしょう。また、生徒用のコンピュータ自体を準備できないのであれば、教師が操作する様子を生徒に見せるだけでも考察を進めることはできます。
　扱う題材は、プレテストで考察した二次関数で定数項が０であるものです。単純化、関数の和のグラフとしての解釈、GeoGebraによる試行錯誤によって、グラフの構造の本質を理解しやすくなります。詳細は表の「授業の目標」「学習活動」「授業で扱う問題」などを参照してください。
　このような二次関数の問題では、平方完成による解法が標準的ですが、代数計算だけで本質を捉えることは簡単ではありません。今回の授業では、証明するだけでなく、GeoGebraを利用して、生徒自身が試行錯誤しながら、関数の和のグラフとして捉えて考察することを主題としています。
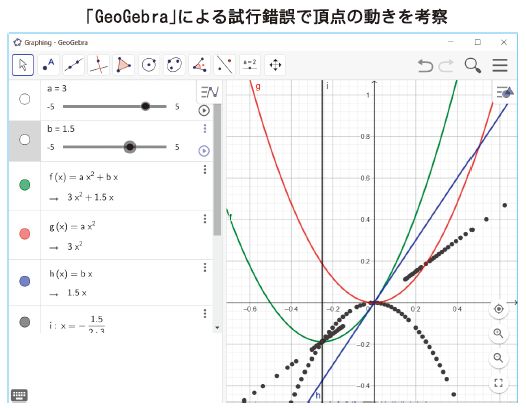
　まず、y＝ax〔2〕＋bxのグラフｆが、y＝ax〔2〕のグラフｇを平行移動したもので、y＝bxのグラフｈに原点で接する（一点のみを共有する）ことに気付くはずです＝下のグラフ。これは関数の和のグラフとして捉えれば、微分に頼らなくても、感覚的に理解できるでしょう。また、係数の値を変化させたとき、頂点の大まかな位置も予想できます。
　次に、頂点の位置を確定していきます。ｆとｘ軸の交点のｘ座標は、ax〔2〕＋bx＝0⇔―ax〔2〕＝bxによって求められるので、ｇとｈのｙ座標の和が０になる位置としてだけでなく、放物線y＝ax２乗とｈが交わる位置として捉えることもできます。実際にGeoGebraで放物線y＝ax〔2〕を表示すると正しいことが確認できます。
　またｘ座標の値は０と―b/aなので、放物線の対称性から、これらの平均、すなわち―b/2aがｆの軸のｘ座標の値となり、放物線と軸の交点として頂点が表示できます。「残像の表示」を利用して係数の値を変化させれば、頂点の動きがどのようになるかは容易に予想できるので、「GeoGebraによる確認」「標準的な証明」「他の考え方」の順で生徒に考察させていきます。

　「他の考え方」では、数学的に面白い発想をしている生徒にクラスの前で説明してもらい、全員で共有します。説明することで本人の考えがまとまり、それを聞いた他の生徒から、さらに新たな発想が生まれることも珍しくありません。
　このような授業の実践において、教員には、新たな発想が生まれるような教材とクラスの雰囲気をつくり、生徒の発想をまとめて、他の生徒にも理解させる力が求められます。生徒の説明が分かりにくかったり、不十分であったり、とっぴな発想で誰も理解できなかったりすることもあるからです。
　筆者の勤務校の数学科では、授業内容に関係するリポートを生徒が自由に提出してよいという文化があり、授業時間内で収まり切らないような生徒の発想を回収・整理し、扱った教材と共に教科会で共有しています。各学校で教えている生徒に合った良質な教材を開発・共有し、積極的に実践していくことが、今後につながっていくのではないでしょうか。
　※本文中の〔2〕は二乗を指す。